Danni

Danni

Sometimes write stuff.

There’s no place like a perfectly Self-balanced BST

10 minute read

“*Trees *Trees *Trees”

The title joke is shamelessly borrowed from the good old classic “There’s no place like 127.0.0.1”

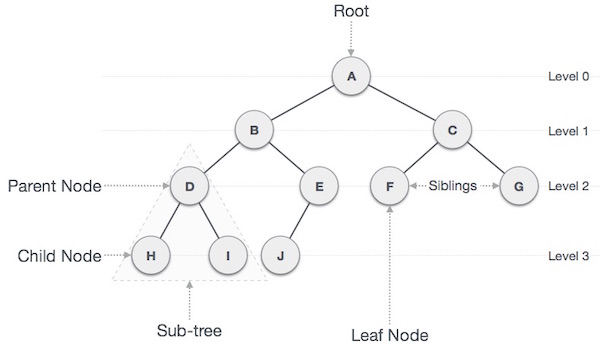
What is Tree

Tree is a heavily used data structure in Computer Science. It’s easy to picture – just a root value and subtrees of children with a parent node, represented as a set of linked nodes(thanks wiki). They are non-linear data structure since data is not stired in a linear way, but hierarchically. It has following properties:

  1. One node is marked as Root node.

  2. Every node other than the root is associated with one parent node.

  3. Each node can have an arbiatry number of child node.

Creating a tree in Python3:

class TreeNode:
    def __init__(self, data):
        self.value = data
        self.left = None
        self.right = None

Types

Binary Tree

A tree whose elements have at most 2 children is called a binary tree Binary Tree A Binary Tree example

Full Binary Tree

A binary tree in which every node other than leaves has two children. 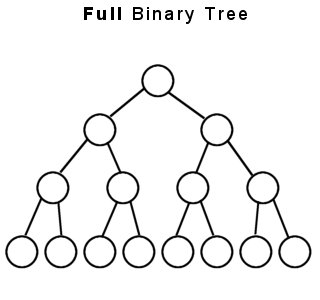Full Binary Tree Full Binary Tree

Complete Binary Tree

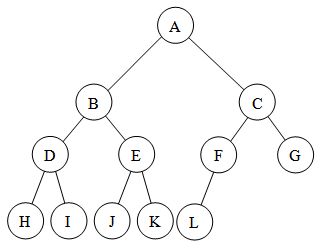
A binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. Complete Binary Tree

Binary Search Tree

Binary search trees (BST), sometimes called ordered or sorted binary trees, it has following properties:

  1. The left subtree of a node contains only nodes with keys lesser than the node’s key.

  2. The right subtree of a node contains only nodes with keys greater than the node’s key.
  3. The left and right subtree each must also be a binary search tree.

There must be no duplicate nodes

  Average Worst
Space O(n) O(n)
Search / Insert / Delete O(logn) O(n)

Binary Search Tree Binary Search Tree

Search a key in BST

First compare with root, then recur for the left or right tree.

def search(root, key):
  if root is None or root.value == key:
    return root

  if root.val < key:
    return search(root.right, key)
  else:
    return search(root.left, key)
Insert a node in BST

A new key is always inserted at leaf. We start searching a key from root till we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.

          11                                11
        /   \        Insert 40            /    \
      20     12    --------->          20      12
     /  \                              /  \  
    10   30                           10   30
                                              \
                                              40

def insert(root, node):
  if root is None or root.value == key:
    root = node
  
  if root.val < node.val:
      if root.right is None:
          root.right = node
      else: 
          insert(root.right, node)
  else: 
      if root.left is None:
          root.left = node
      else: 
          insert(root.left, node)
Delete a node in BST

  1. delete leaf node: Simply remove from the tree.

  2. delete node has only one child: Copy the child to the node and delete the child

  3. delete node has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor. Note that inorder predecessor can also be used.

         50                            60
      /     \         delete(50)      /   \
    40      70       --------->    40    70 
           /  \                            \ 
          60   80                           80

The important thing to note is, inorder successor is needed only when right child is not empty. In this particular case, inorder successor can be obtained by finding the minimum value in right child of the node.

Inseresting facts:

  1. Inorder traversal of BST always produces sorted output.
  2. We can construct a BST with only Preorder or Postorder or Level Order traversal. Note that we can always get inorder traversal by sorting the only given traversal.
  3. Number of unique BSTs with n distinct keys is Catalan Number
BST Traversal
Traversal Methods Details
DFS
Stack		 1. Pre order: root - left- right
2. In order: Left - root - right
3. Post order: Left - right -root
BFS
Queue: need to track status		 Level Order Traversal: Left to right

Self-balanced Binary Search Tree

Self-Balancing Binary Search Trees are height-balanced binary search trees that automatically keeps height as small as possible when insertion and deletion operations are performed on tree. The height is typically maintained in order of Log n so that all operations take O(Log n) time on average.

Why we need self-balanced BST?

In short, to improve operation performance.

There are some edge cases where inserting ordered data in BST results in a single list, which makes the lookup time O(n). So to avoid all this vases, we want the BST as balanced as possible – number of nodes on left and right tree do not differ too much.

Red Black Tree

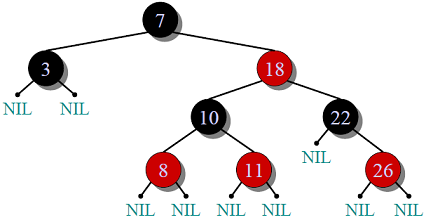Red Black Tree Red Black Tree

Red-Black Tree is a self-balancing Binary Search Tree (BST) where every node follows following rules.

  1. Every node has a color either red or black.

  2. Root of tree is always black.

  3. There are no two adjacent red nodes (A red node cannot have a red parent or red child).

  4. Every path from a node (including root) to any of its descendant NULL node has the same number of black nodes.

Every Red Black Tree with n nodes has height <= 2Log2(n+1)

Why Red-Black Trees?

Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of a Red-Black tree is always O(Logn) where n is the number of nodes in the tree.

Red Black Tree V.S. AVL Tree

The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search more frequent, then AVL tree should be preferred over Red-Black Tree.

AVL Tree

AVL Tree AVL Tree

AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

Why AVL Tree?

Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree.

METRIC Red Black Tree AVL Tree  
Insertion(Worst Case) O(1) O(logn)  
Max Tree Height 2 * Log(n) 1.44 * Log(n)  
Search(Worst) O(logn) O(logn)  
Deletion(Worst) O(logn) O(logn)  
Used when always when frequent lookup required  
Real world application Multiset, Multimap, Map, Set, etc DB Transactions  

Q TIME

Binary Tree Paths

def binaryTreePaths(self, root):
    paths = []
    path = ""
    helper(root, path, paths)
    return paths

def helper(self, node, path, paths):
    if node is None:
        return path
    if node.left or node.right:
        # result.append("->")
        path = path + str(node.val) + "->"
    else:
        paths.append(path + str(node.val))
    helper(node.left, path, paths)
    helper(node.right, path, paths)

Validate BST

  1. Recursion: use in order traversal of BST.
def isBST(root):
  out = []
  inOrder(root, out)

  for i in range(1, len(out)):
    if out[i] <= out[i-1]:
      return False
  return True

  for i in range(1, len(out)):

def inOrder(root, out):
  if not root:
    return
  self.inOrder(root.left, out)
  out.append(root.val)
  self.inOrder(root.right, out)

Validate Full BST

  1. Iteration
def isFullBST(rot):
  if not root:
    return True
  
  if root.left is None and root.right is None:
    return True

  if root.left is not None and root.right is not None:
    return (isFullBST(root.left) and isFullBST(root.right))

  # when none of above conditions work
  return False

Validate Complete BST

DO Level Order Traversal from the root.

  1. We can define a term “Full node” whose both cildren nodes are not empty or not NULL. Then once one node found not be a “full node”, then every other node on the same level must be leaf nodes.
  2. If the left children node is empty, then right one MUST be empty.
def isCompleteBST(root):
  if root is None:
    return True
  queue = []
  flag = False  # record not FULL node

  queue.append(root)
  while(len(queue) > 0):
    tempNode = queue.pop(0) # Dequeue
      if (tempNode.left):
        if flag == True:
          return False
        queue.append(tempNode.left)  # enque left child
      else:
        flag = True
  
      if(tempNode.right):
        if flag == True:
          return False
        queue.append(tempNode.right)
        else: 
            flag = True
    return True

BST Level Order Traversal

  1. Iteration(BFS)

Of course stack for iterative methods:

def levelOrder(root):
  if not root:
    return
  
  res = []
  queue = collections.deque() 
  # deque is preferred over list when
  # quicker append and pop from botth ends need
  # both O(1)
  # implemented as a doubly linked list of block node
  # so good for random-access and fixed length operations
  queue.append(root)
  while queue:
    level = []
    for i in range(len(queue)):
      node = queue.popleft()
      level.append(node.val)
      if node.left:
        queue.append(node.left)
      if node.right:
        queue.append(node.right)
    res.append(level)
  return res
  1. recursion(BFS)

Recursion method is still just defining another helper function.

def levelOrder(root):
    res = []
    dfs(root, 0, res)
    return res

def dfs(root, depth, res):
    if root == None:
        return res
    if len(res) < depth+1:
        res.append([])
    res[depth].append(root.val)
    self.dfs(root.left, depth+1, res)
    self.dfs(root.right, depth+1, res)

BST Pre Order Traversal

  1. recursion Easy to define a helper function to help with recursion.
def inOrder(root):
  if not root:
    return
  out = []
  helper(root, out)
  return out

def helper(root, out): # helper func bcoz need to append result
  if root:
    out.append(root.val)
    inOrder(root.left, out)
    inOrder(root.right, out)
  return out
  1. iteration

note signe.

def preOrder(root):
  if not root:
    return
  
  stack = [root]
  out = []
  while(len(stack) > 0):
    node = stack.pop()
    if node.right is not None:
      stack.append(node.right)
    if node.left is not None:
      stack.append(node.left)

BST In Order Traversal

  1. recursion Same as before, recursion’s syntax is much more concise.
def inOrder(root):
  out = []
  helper(root, out)
  
def helper(root, out):
  if root:
    helper(root.left, out)
    out.append(root.val)
    helper(root.right, out)
  1. iteration
def inOrder(root):
  if not root:
    return
  
  out = []
  stack = [root]
  visited = set()
  # need to track status, ortherwise will not be able to come back

  while stack:
    curr = stack.pop()
    if curr not in the visited:
      visited.add(curr)
      if curr.right:
        stack.append(curr.right)
      if curr.left:
        stack.append(curr.left)
    else:
      out.append(cuur.val)
  return out

BST Post Order Traversal

  1. recursion The easiest way is recursion method. 
    def postOrder(root):
  if not root:
 return []
# aaaaa
  2. iteration ```python ans = []

def postOrderIterative(root): # edge case if root is None: return

stack = []

while(True): while (root): if root.right is not None: stack.append(root.right) stack.append(root)

  root = root.left

root = stack.pop()

if (root.right is not None and
  peek(stack) == root.right):
  stack.pop() 
  stack.append(root)
  root = root.right
else:
  ans.append(root.data) 
  root = None

if (len(stack) <= 0):
  break ``` ###### DFS Recursion Explained

Recursion is definitely an elegant way to solve questions but there’s one down side woth the memory usage.

Stack + recursion == messy memory performance

BST Zigzag Order Traversal


# Time Complexity: O(n)
# Space Complexity: O(n)+(n)=O(n)

    def zigzagLevelOrder(self, root):
        
        if not root: return []
        
        result = []
        queue = [(root, 0)]
        
        while queue:
            node, lvl = queue.pop(0)
            if len(result) <= lvl:
                result.append([node.val])
            else:
                if lvl % 2 == 0:
                    result[lvl].append(node.val)
                else:
                    result[lvl].insert(0, node.val)
            if node.left: queue.append((node.left, lvl+1))
            if node.right: queue.append((node.right, lvl+1))
        
        
        return result

Symmetric Tree

  1. recursion
  def isSymmetric(self, root):
    return isMirror(root, root)
  
  def isMirror(root1, root2):
    if not root1 and not root2:
      return True
    if not root1 or not root2:
      return False
    return (root1.val == root2.val) and isMirror(root1.left, root2.right) and isMirror(root1.right, root2.left)
  1. iteration
if not root:
  return True
stackl, stackr = [root.left], [root.right]
while len(stackl) > 0 and len(stackr) > 0:
  left = stackl.pop()
  right = stackr.pop()
  if not left and not right:
    continue
  elif not left or not right:
    return False
  if left.val != right.val:
    return False
  stackl.append(left.left)
  stackl.append(left.right)
  stackr.append(right.right)
  stackr.append(right.left)
return len(stackl) == 0 and len(stackr) == 0

Same Tree

  1. Iteration
def isSameTree(p, q):
  stack = [(p, q)]
  while stack:
    p, q = stack.pop()
    if p == None and q == None:
        continue
    if p == None or q == None
        return False
    if p.val == q.val:
        stack.append((p.right, q.right))
        stack.append((p.left, q.left))
    else:
        return False
  return True
  1. Recursion
def isSameTree(p, q):
  if not p and not q:
    return True
  elif not p or not q:
    return False
  else:
    return p.val == q.val and isSameTree(p.left, q.left) and isSameTree(p.right, q.right)

Maximum Depth of BST

  1. Iteration 
    def maxDepth(root):
 if not root:
     return 0
 temp = [root]
 depth = 0

 while temp:
     new_level = []
     depth +=1
     for node in temp:
         if node.left:
             new_level.append(node.left)
         if node.right:
             new_level.append(node.right)
     temp = new_level
 return depth
  2. Recursion 
    def maxDepth(root):
 if root is None:
     return 0
 else: 
     left_height = self.maxDepth(root.left)
     right_height = self.maxDepth(root.right)
     return max(left_height, right_height) + 1

    BST Path Sum

How to find path sum from root to leaf that equals to given sum?

  1. iteration
def pathSum:
  if not root:
    return
  out = []
  stack = [(root, [root.val], root.val)]

  while stack:
    root, path, s = stack.pop()
    if not root.right and not root.left:
      if s==sum:
        out.append(path)
    if root.left:
      stack.append((root.left,path+[root.left.val],s+root.left.val))
    if root.right:
      stack.append((root.right,path+[root.right.val],s+root.right.val))
  return out
Reference

Huge thanks to Tutorials Point, G4G, Quora and Zhihu for the information.

Leave a comment

You may also enjoy